Current and voltage relationships

The non-linear relationship between current and voltage is important but easy to understand.

In this section we explore the following topics.

IV curves

A device’s IV curve – current versus voltage curve – is a graph of the current that will flow in the device as a function of the voltage across it. As suggested by Ohm’s Law, , the relationship between current and voltage in a resistor is linear. Figure 1 clearly shows that the current increases linearly with increasing … Continue reading

'Resistance' of an LED

LEDs do not have a linear relationship between current and voltage so they cannot be modeled as simply as a resistor using Ohm’s Law, . We can, however, make a simplification and model them over a range of currents as a combination of a resistor and a voltage source. If we look at a typical … Continue reading

Loadline resistance graphic tool

Most LED circuits require a current limiting resistor. The loadline calculator makes resistor selection very simple. Example 1: Chose a resistor to give 20 mA on a yellow LED and 5 V supply. Solution: Choose 20 mA on the If axis. Slide across to the yellow LED curve. Find the nearest loadline: in this case it’s … Continue reading

Variations in Vf and "binning"

LEDs’ forward voltage drop varies from device to device and by more than you might think. This causes a few issues for the user. The Lite-On LTST-C170TBKT InGaN blue LED datasheet, for example, shows the forward voltage varies between 2.8 V and 3.8 V at 20 mA. This is quite a variation. The lower value would, just about, allow … Continue reading

Power calculations

Power calculations are required to ensure that devices operate within the manufacturers specified limits. In most cases these only require a single multiplication or division.

Power is measured in watts (W) or milliwatts (mW).

Given V and I …

Power in an electrical circuit is given by

$P = VI$

where P is power (watts or W), V is voltage (volts or V) and I is current (amps or A).

Example 1

I have a 12 V LED strip which requires 170 mA. How many watts is that?

$P = VI = 12 \times 0.17 = 2.04 \, \mathrm W$

Answer: 2 W.

Burnt resistor. Too much power and the smoke gets out. — A burnt resistor – the result of attempting to dissipate too much power in an under-rated component. A 1/4 W resistor would not last long at 2 W.

Given I and R …

From Ohm’s law we know that $ V = IR $ so

$P = VI = IRI = I^2R$

Example 2

There is 120 mA flowing through a 22 Ω resistor in my circuit. Will a 0.5 W resistor be able to dissipate the heat?

$P = I^2R = 0.12^2 \times 22 = 0.32 \, \mathrm W$

Answer: This is comfortably inside the 0.5 W rating.

Given V and R …

From Ohm’s law again we know that $ I = \frac {V}{R} $ so

$P = VI = V \frac {V}{R} = \frac {V^2}{R}$

Example 3

I need to drop 10 V to feed an LED from a 12 V power supply. The resistor value is 490 Ω.

Q1. How much of my battery power will be wasted in the resistor?

$P = \frac {V^2}{R} = \frac {10^2}{490} = 0.204\, \mathrm W $

Answer: 0.2 W. A ¼ W resistor should be fine.

Q2. How much power will be dissipated in the LED? (Assume 2 V is dropped across the LED.)

Answer: First we need to calculate the current through the 490 Ω resistor.

$I = \frac {V}{R} = \frac {10}{490} = 20.4\, \mathrm mA $

Now we can calculate the power:

$P = VI = 2 \cdot 20m = 40 \, \mathrm mW$

5/6 or 83% of the power is “wasted” in the resistor.

Ohm’s law – LED resistor calculation

Ohm’s law states that the current through a resistive conductor (a resistor) between two points is directly proportional to the voltage across the two points.

$I={\frac {V}{R}}$ where I is current (amps or A), V is voltage (volts or V) and R is resistance (ohms or $\Omega$).

Example 1 – resistor calculation

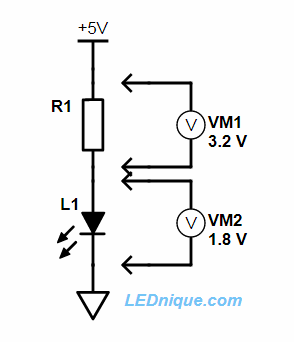
Resistor and LED. — Figure 1. Series connection of a resistor and LED. The voltmeters show the voltage drop across each element of the circuit.

I have a 5 V supply and I want to run a red LED at 8 mA.

We can see from the LED’s IV curve that at 8 mA the red LED will have a forward voltage of 1.8 V. That means there’s 5 – 1.8 = 3.2 V across the resistor. Using Ohm’s law we can calculate the resistance.

$$ I = \frac {V}{I} = \frac {3.2}{0.008} = 400~\Omega $$

390 $\Omega$ is the closest standard value and that will be fine.

Don’t forget to check the power rating of the resistor! See Power calculations.

Notes

Note that the order of the components in this example doesn’t matter. The resistor can go between the +5 V supply and the LED or between the LED and ground. The same current will flow through the circuit and the same voltage drop will occur on the LED.