For various reasons it is often necessary to control LEDs supplied by a voltage higher than the micro-controller can supply or withstand. In these cases the most common solution is to use an NPN transistor as a switch or driver to buffer between the two parts of the circuit – the low-voltage control circuit and the high-voltage load circuit.
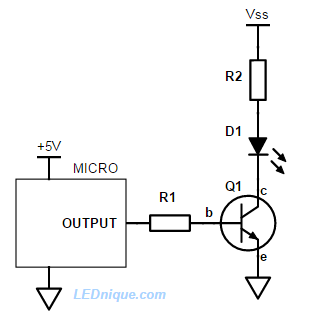
When there is no current flowing into the base (b) of Q1 the transistor is off and no current flows from the collector (c) to the emitter (e). As we increase the current into the base of the transistor the transistor starts to turn on and its resistance falls allowing current to flow from Vss, through R2, D1 and Q1 to ground.
Small signal transistors have a “current gain” of 50 to 300. This means that for 0.1 mA into the base we should be able to get 5 to 30 mA to flow through the collector. The relationship is given by the equation \( I_C = h_{FE}I_B \) where \( I_C \) is the collector current, \( h_{FE} \) is the current gain and \( I_B \) the base current.
At first glance it seems that we could control the LED current to any value we wanted by controlling the base current. Unfortunately there is enough variation between transistors and the fact that this parameter is temperature dependent that this would not be a good reliable and repeatable design. (It might be OK for a one-off project provided you were confident you would never have to replace the transistor.)
Instead we inject more than enough current into the base to turn the transistor “hard” into saturation: the collector voltage drops as low as it can go – typically below 0.2 V.
Example 1 (NPN driver)
- Our micro-controller output is a 5 V signal.
- Vss is 12 V.
- The LED, D1 requires 100 mA and will have a forward voltage of 2.8 V at that current.
- Q1 has a \( h_{FE} \) of somewhere around 100.
R1
We want to ensure that the transistor saturates to give minimum voltage drop between the collector and emitter. In saturation we’ll assume that a current gain of 10 to 20 is likely. To guarantee saturation we should design for a base current of 5 to 10 mA. This will be fine for most micro-controllers (but always check the specification). The base voltage will rise to about 0.6 V when forward biased so the voltage across R1 will be 5 – 0.6 = 4.4 V. We can calculate (from Ohm’s Law) \( R_1 = \frac {V}{I} = \frac {4.4}{0.005} = 880\,\Omega \) and it would be half of that at 10 mA. We can go somewhere in-between with a 560 Ω or 680 Ω resistor.
R2
\( \begin{align} V_{R2} & = V_{SS} – V_{LED} – V_{Q1} \\ & = 12 – 2.8 – 0.2 \\ & = 9\,V \end{align} \)\( \begin{align} R2 & = \frac {V}{I} \\ & = \frac {9}{0.1} \\ & = 90\,\Omega \end{align}\)

